Não seja um Ateu.

Números Complexos na Casio fx-82MS Usual em Máquinas Elétricas - Parte 2

Números Complexos na Casio fx-82MS Usual em Máquinas Elétricas - Parte 1

# Frase do Dia ( :

A Matemática é a mais simples, a mais perfeita e a mais antiga de todas as ciências.

(Jacques Hadarmard)

Descontraindo :)

Números Complexos na Eletricidade

Acima apresentamos os quatro quadrantes trigonométricos. Veja a posição do ângulo do vetor

1° Quadrante: 0° < 90°

2° Quadrante: 90° < 180°

3° Quadrante: 180° < 270°

4° Quadrante: 270° < 360° = 0°

Devemos que o eixo x ou R deverá ser representado como o Eixo dos n°s reais. Já o eixo y ou J, representaremos o eixo dos n°s imaginários. Observe que - 45° = 315°. Um ângulo negativo na verdade, corresponde a 360°, uma volta completa, no sentido anti-horário, menos o dito ângulo. No ângulo negativo, você parte do 0°, girando no sentido horário, e no ângulo positivo, você parte do 0°, no sentido anti-horário. Assim, o ângulo de 315°, no sentido anti-horário, é a mesma posição de -45°, no sentido horário.

Simbolizamos um Vetor utilizando uma letra maiúscula acompanhado de um acento circunflexo, seta ou ponto, sobre a letra. Veja um exemplo:

Representações de um Vetor.

> Forma Polar: |E| |_Ø__

> Forma trigonométrica: |E| x cos Ø + J |E| x sin Ø

> Forma cartesiana: Ex + J Ey

É importante ressaltar que estas formas representam um mesmo vetor. Com qualquer uma chegamos às outras.

|E| ---> módulo

Ø ---> ângulo

Ex ---> Parte Real (coordenada no eixo x)

Ey ---> Parte imaginária (coordenada no eixo y)

Agora vamos realizar a transformação Polar para Cartesiana e vice - versa.

Polar para Cartesiana:

|E| |_Ø__ ---> |E| x cos Ø + J |E| x sin Ø ---> Ex + J Ey

Ex 1: Vetor: 5 |36,87° ---> 5 x cos 36,87° + J 5 x sin 36,87° = 4 + J3

Desta forma: 5 | 36,87° = 4 + J3

Desta forma, observamos que se passa pela forma trigonométrica para chegar a forma cartesiana.

Cartesiana para Polar :

Ex + J Ey ---> |E| = raí quadrada de ( Ex2 + Ey2 ) e Ø = arc tg Imaginário(Ey) / Real ( EX)

Agora já podemos pensar em praticar algumas operações como adição, subtração, multiplicação e divisão.

Soma

Os vetores têm que estar na forma cartesiana. Soma-se as partes reais e as partes imaginárias separadamente.

	Parte Real	Parte Imaginária
Vetor 1	5	+ J7
+ Vetor 2	6	+ J4
+ Vetor 3	1	+ J2
Soma	12	+ J13

O resultado é 12 + J13 (é um vetor que está no 1° quadrante, porque tanto a parte real, como a imaginária é positiva). 0° < Ø <90°.

	Parte Real	Parte Imaginária
Vetor 1	- 2	+ J 4
+ Vetor 2	3	+ J – 2
+ Vetor 3	- 5	+ J -8
Soma	- 4	+J -6

O resultado é - 4 - J6 (é um vetor que está no 3° quadrante, porque tanto a parte real, como a imaginária são negativas. 180° < Ø <270° .

Subtração

	Parte Real	Parte Imaginária
Vetor 1	- 5	+ J 6
- Vetor 2	2	+ J 3
Soma	- 7	+ J 3

O resultado é - 7+ J3 (é um vetor que está no 2° quadrante, porque a parte real, é negativa, e a imaginária positivas. 90° < Ø <180°

	Parte Real	Parte Imaginária
Vetor 1	6	+ J -7
- Vetor 2	1	+ J - 2
- Vetor 3	3	+ J - 1
Soma	2	+ J - 4

O resultado é 2 - J4 ( é um vetor que está no 4° quadrante, porque a parte real, é positiva, e a imaginária negativa. 270° < Ø <360° ou 0°

Divisão e Multiplicação:

Os vetores têm que estar na forma polar. Multiplica-se os módulos e soma-se os ângulos no caso da multiplicação e divide-se os módulos e subtrai-se os ângulos, no caso da divisão.

Ex.1:

3|_45°__ X 5 |_120°__ = 3 X 5 |_45°__+__120°__ = 15 |_165°__

Ex. 2 :

4 !_340°__ / 2 |_60°__ = 4 /2 |_340°__-__60°__ = 2 |_280°__

Alguns exemplos práticos em corrente alternada

Impedância:
Normalmente é dada na forma cartesiana, onde a parte real corresponde a resistência do fio ( R) e a parte imaginária é a reatância ( capacitiva - Xc ou indutiva - XL). Para multiplicar a impedância por uma corrente, p.ex., é necessário primeiro transformar a indutância na forma polar, o que permite sua multiplicação e divisão. Para dividir uma tensão por uma impedância também temos que por a impedância na forma polar.

R = 5 Ohms, XL = 10 Ohms

Z = Raíz quadrada de ( 25 + 100 )

Ø = arc tg 10/5 = arc tg 2 = 63,4°

Z = 11,18 |_ 63,4°__ .Nesta forma, posso multiplicar esta impedância por uma corrente ou dividir uma tensão por ela.

Lembre-se: V = Z x I e I = V / Z

Tensão e corrente:

É mais comum vermos estas grandezas elétricas na forma polar. Para somarmos ou subtrairmos duas, ou mais, correntes ou tensões, primeiro temos que transformá-las na forma cartesiana.

Ex. I = 30 |_ 45°__ Amperes

Ix = 30 x cos 45 = 30 x 0,787 = 23,61 amperes (eixo x)

Iy = 30 x sin 45 = 30 x 0,787 = 23,61 amperes ( eixo y)

I = 30 |_ 45°__ Amperes = 23,61 + J 23,61 amperes. Agora posso somar esta corrente a outra corrente, que também esteja na forma cartesiana.

Potência:

Em corrente alternada existem três potências. Potência aparente(S), Potência ativa(P) e Potência reativa(Q). A potência aparente ( VA) é o módulo e ângulo do vetor potência. A potência ativa (WATTS) é a componente real do vetor potência. A potência reativa é a componente imaginária do vetor potência. Na literatura elétrica ou em manuais de fabricantes é comum vermos dado somente a potência ativa (Watts), mais o cos Ø. Note que neste caso, não nos foi fornecido nem a forma polar nem a cartesiana, mas sim um híbrido das duas formas. Foi dado a parte real da forma cartesiana mais o cos do ângulo da forma polar. Neste caso o primeiro passo é encontrar a forma polar por inteiro S = |S| |_Ø__ . Sabemos, na conversão de polar para cartesiana que P = |S| x cos Ø, então |S| = P / cos Ø e Ø = arc cos ( cos Ø dado ). Para achar Q , fazemos Q = |S| x sin Ø . Agora, temos a forma polar e a cartesiana da potência. Podemos somá-la com outra potência, dividi-la pela corrente para encontrar a tensão, etc. Lembre-se que S (Potência CA) = VI

Ex. Motor: P = 10000 Watts e cos Ø.

Encontrar a potência aparente e a reativa do motor. |S| = P / cos Ø ---> |S| = 10000 / 0,6 = 16666 VA ( Volt x Ampere)

Ø = arc cos (cosØ dado) ---> arc cos 0,6 = 53,13°

Q = |S| x sin Ø ---> 16666 x 0,7999 = 13 333 VAr ( Volts x Amperes reativo )

forma polar ---> S = 16666 |_ 53,13°__

forma cartesiana ---> S = 10000 + J 13333

Agora, na forma cartesiana podemos somar as duas potências, p. ex. e na forma polar, dividir a potência encontrada pela tensão da rede, para achar a corrente, p.ex. Veja que, que em CA, todas as grandezas são vetoriais ( Z-impedância , Resistência, X-reatância, V-tensão, I-corrente, S-potência aparente, P-potência ativa, Q-potência reativa ,etc). Não se esqueça que R(Ohms) e P(Watts) são vetores com ângulo zero e X(Ohms) e Q(VAr) com ângulo + 90°.

# Frase do Dia ( :

A História mostra que os chefes de império que encorajaram o culto das Matemáticas, fonte comum de todas as ciências exatas, são também aqueles cujo reinado foi mais brilhante e cuja glória é mais duradoura.

(Miches Charles)

Gabarito:

1) B
2) D
3) A
4) A
5) A
6) E

Agora que estudamos a teoria, vamos tentar resolver os seguintes exercicios:

01 - UEFS-92.1 - O valor da expressão E = x^-1 + x², para x = 1 - i , é:
a)-3i
b)1-i
c) 5/2 + (5/2)i
d) 5/2 - (3/2)i
e) ½ - (3/2)i

02 -UEFS-93.2 - Simplificando-se a expressão E = i⁷ + i⁵ + ( i³ + 2i⁴ )² , obtêm-se:
a) -1+2i
b) 1+2i
c) 1 - 2i
d) 3 - 4i
e) 3 + 4i

03 - UEFS-93.2 - Se m - 1 + ni = (3+i).(1 + 3i), então m e n são respectivamente:
a) 1 e 10
b) 5 e 10
c) 7 e 9
d) 5 e 9
e) 0 e -9

04 - UEFS-94.1 - A soma de um numero complexo z com o triplo do seu conjugado é igual a -8 - 6i. O módulo de z é:
a) Ö 13
b) Ö 7
c) 13
d) 7
e) 5

05 - FESP/UPE - Seja z = 1+i , onde i é a unidade imaginária. Podemos afirmar que z⁸ é igual a:
a) 16
b) 161
c) 32
d) 32i
e) 32+16i

06 - UCSal - Sabendo que (1+i)²² = 2i, então o valor da expressão
y = (1+i)⁴⁸ - (1+i)⁴⁹ é:
a) 1 + i
b) -1 + i
c) 2²⁴ . i
d) 2⁴⁸ . i
e) -2²⁴ . i

Divisão de Números Complexos na Forma Binômia:

Regra : Para dividir um número complexo z por outro w ¹ 0 , basta multiplicar numerador e denominador pelo complexo conjugado do denominador .
Ex: = =

Conjugado de um Número Complexo

Dado um número complexo z = a + bi , chama-se conjugado de z e representa-se por 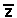, a um outro número complexo que possui a mesma parte real de z e a parte imaginária o simétrico aditivo da parte imaginária de z .z = a + bi ® 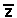= a - bi
Ex: z = 3 + 5i ;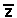 = 3 - 5i

Obs : Sabemos que os números complexos podem também ser representados na forma de pares ordenados . Assim é que z = a + bi = (a,b).

Portanto , por analogia com o sistema de coordenadas cartesianas , pode-se representar graficamente qualquer número complexo z num sistema de coordenadas cartesianas , bastando marcar a parte real a no eixo horizontal e a parte imaginária b no eixo vertical . Neste caso , o eixo horizontal é chamado eixo real e o eixo vertical é chamado eixo imaginário. O plano cartesiano, neste caso , denomina-se plano de Argand-Gauss.
O ponto que representa o número complexo z , denomina-se afixo de z.

Exercícios resolvidos

1) Sendo z = (m² - 5m + 6) + (m² - 1) i , determine m de modo que z seja um imaginário puro.

Solução: Para que o complexo z seja um imaginário puro, sua parte real deve ser nula ou seja, devemos ter
m² - 5m + 6 = 0, que resolvida encontramos m=2 ou m=3.

2) Determine a parte real do número complexo z = (1 + i)¹² .

Solução: Observe que (1 + i)¹² = [(1 + i)²]⁶ . Nestas condições, vamos desenvolver o produto notável
(1 + i)² = 1² + 2.i + i² = 1 + 2i -1 = 2i \ (1 + i)² = 2i (isto é uma propriedade importante, que vale a pena ser memorizada).
Substituindo na expressão dada, vem:
(1 + i)¹² = [(1 + i)²]⁶ = (2i)⁶ = 2⁶.i⁶ = 64.(i²)³ = 64.(-1)³ = - 64.
Portanto, o número complexo dado fica z = - 64 = - 64 + 0i e portanto sua parte real é igual a -64.

3) Determine a parte imaginária do número complexo z = (1 - i)²⁰⁰ .

Solução: Podemos escrever o complexo z como: z = [(1 - i)²]¹⁰⁰ . Desenvolvendo o produto notável
(1 - i)² = 1² - 2.i + i² = 1 - 2i -1 = - 2i \ (1 - i)² = - 2i (isto é uma propriedade importante, que merece ser memorizada).
Substituindo na expressão dada, vem:
z = (- 2i)¹⁰⁰ = (- 2)¹⁰⁰. i¹⁰⁰ = 2¹⁰⁰ . i¹⁰⁰ = 2¹⁰⁰ . ( i² )⁵⁰ = 2¹⁰⁰. (- 1)⁵⁰ = 2¹⁰⁰ . 1 = 2¹⁰⁰.
Logo, o número complexo z é igual a 2¹⁰⁰ e portanto um número real. Daí concluímos que a sua parte imaginária é zero.

Número Complexo

Definição: Dados dois números reais a e b, define-se o número complexo z como sendo:
z = a + bi, onde i = Ö-1 é a unidade imaginária.
Exs: z = 2 + 3i (a = 2 e b = 3)
w = -3 -5i (a = -3 e b = -5)
u = 100i ( a = 0 e b = 100)

NOTAS:
a) diz-se que z = a + bi é a forma binômia ou algébrica do complexo z .
b) dado o número complexo z = a + bi , a é denominada parte real e b parte imaginária.
Escreve-se: a = Re(z); b = Im(z).
c) se em z = a + bi tivermos a = 0 e b diferente de zero, dizemos que z é um imaginário puro. Ex: z = 3i.
d)se em z = a + bi tivermos b = 0 , dizemos que z é um número real .
Ex: z = 5 = 5 + 0i.
e)do item (c) acima concluímos que todo número real é complexo, ou seja,
o conjunto dos números reais é um subconjunto do conjunto dos números complexos.
f) um número complexo z = a + bi pode também ser representado como um par ordenado z = (a,b).

# Frase do Dia ( :

Na Matemática, se a experiência não intervém depois que se deu o primeiro passo, é porque não é mais preciso.

(Pontes de Miranda)

Potências de i :

i⁰ = 1
i¹ = i
i² = -1
i³ = i² . i = -i
i⁴ = (i²)² = (-1)² = 1
i⁵ = i⁴ . i = 1.i = i
i⁶ = i⁵ . i = i . i = i² = -1
i⁷ = i⁶ . i = -i , etc.

Percebe-se que os valores das potências de i se repetem no ciclo
1, i, -1, -i, de quatro em quatro a partir do expoente zero.
Portanto, para se calcular qualquer potência inteira de i, basta eleva-lo ao resto da divisão do expoente por 4. Assim, podemos resumir:

i⁴ⁿ = i^r onde r = 0 , 1 , 2 ou 3. (r é o resto da divisão de n por 4).

Exemplo: Calcule i²⁰⁰¹
Ora, dividindo 2001 por 4, obtemos resto igual a 1. Logo i²⁰⁰¹ = i¹ = i.

Unidade imaginária

Unidade imaginária: define-se a unidade imaginária , representada pela letra i , como sendo a raiz quadrada de -1.
 Pode-se escrever então:

Observe que a partir dessa definição, passam a ter sentido certas operações com números reais, a exemplo das raízes quadradas de números negativos.

#Frase do Dia ( :

Quem não conhece a matemática morre sem conhecer a verdade científica.

(Schelbach)

Números complexos Vídeo aula - Parte 3

Números Complexos Vídeo aula - Parte 2

Números complexos vídeo aula - Parte 1

Os Números Complexos foram inventados para resolvermos as equações do segundo grau ?

Não ! Isso é uma falácia clássica

Além de historicamente errada, essa extremamente comum "explicação" para o surgimento dos números complexos é um absurdo. Com efeito, por que alguém iria buscar raízes num campo numérico desconhecido?

Até cerca de 1 650 dC, em respeito à orientação geométrica da matemática grega, as únicas raízes consideradas como legítimas ou verdadeiras eram as que correspondiam à grandezas geométricas ou físicas : podiam ser interpretadas como comprimentos, áreas, volumes, massas, etc. Diríamos hoje: correspondiam a números reais POSITIVOS .

Por exemplo, Bhaskara, que foi um dos indianos que mais perto chegou da idéia da moderna álgebra ( conhecia a regra menos vezes menos dá mais, trabalhava com equações de coeficientes negativos, etc ), reconhecia que a equação.

x2 - 45 x = 250

era satisfeita por dois valores, x = 5 e x = - 5, mas dizia que não considera-se a segunda pois as pessoas não apreciam raízes negativas . 

Resumindo, até o surgimento dos cartesianos, c. 1650, as raízes eram divididas em verdadeiras ( correspondiam aos reais positivos) e falsas ( que correspondiam aos reais negativos e não eram consideradas como legítimas ). As únicas e raras ocorrências de raízes negativas nesse período surgiam em problemas de contabilidade, onde eram interpretadas como dívidas.

Como surgiram os números complexos ?

Cardano 1545 ao tentar resolver a cúbica x 3 = 4 + 15x , a qual ele sabia ter raiz verdadeira x = 4, constatou que a regra de dal Ferro-Tartaglia produzia a seguinte expressão ( em notação moderna ) :

Deparando-se com o termo  - 121 , ele não conseguiu ver como "destravar" o calculo, de modo a fazer a regra chegar ao esperado x = 4.

Foram precisos mais de 25 anos para Bombelli, em 1572, atinar como resolver o impasse . Esse disse ter tido a "idéia louca" de operar com as quantidades da forma a + b  -1 sob as mesmas regras que se usa com os números reais, mais a propriedade

(  -1 )2 = -1  

Para assim conseguir "destravar" a regra, fazendo-a produzir o desejado x = 4.

O próprio Bombelli não estava bem seguro do que havia criado, chegando mesmo a dizer que eram uma nova espécie de raízes quadradas ... que tem regras diversas das outras. Para os demais matemáticos da época, os números complexos eram vistos com suspeita e quanto muito tolerados, na falta de melhor coisa. Até o nome que receberam, números SOFÍSTICOS, espelhava bem a situação.  

É de se acrescentar que alguns matemáticos da época procuraram descobrir maneiras de se evitar o uso dos complexos. Entre eles, o que mais procurou evitar as torturas mentais envolvidas com o uso de raízes quadradas de negativos foi Cardano. Em seu difícil livro De Regula Aliza, de 1 570, Cardano procurou inventar artifícios de cálculo que evitassem o uso de raízes quadradas de negativos quando da aplicação das regras de resolução de cúbicas. Conseguiu apenas magros resultados. Foram necessários trezentos anos para que, em 1 890, Capelli conseguisse provar que isso é em geral impossível de conseguir.

O primeiro estudo dos complexos: Bombelli 1 572

Rafael Bombelli gastou 74 páginas de sua L'Algebra para estudar as leis algébricas que regiam o cálculo com as quantidades a + b  -1 . Em particular, mostrou que as 4 operações aritméticas sobre números complexos produzem numeros desse tipo a soma de um real e um imaginário puro não pode se reduzir a um só nome.

Investigação do fechamento dos complexos

Embora Bombelli já tivesse se preocupado em provar o fechamento das operações aritméticas com números complexos, em 1 680, encontramos ninguêm menos do que Leibniz questionando-se se seria real ou não o resultado de  

( a + ib ) + ( a - ib )

Lambert, em 1 750, mostrou que  i  ,  i i ,etc todos tem a forma a + ib.

Extensão das operações transcendentes aos complexos:

A principal dificuldade foi entender o logaritmo de números complexos. E se vamos falar do ln z, por que não falar no log de reais negativos ? Com efeito, estendeu-se por muitos anos a polêmica do significado e valor do ln (-1). Nada menos do que Leibniz, Euler e J. Bernoulli entraram na briga.

Bernoulli alegava que, como 1 2 = (-1) 2, tomando o log, obtemos 0 = ln(-1). Leibniz dizia que isso não pode ser correto, uma vez que teríamos, de ln(-1) = 0, que -1 = e 0 = 1.

O passo decisivo foi dado por Euler que mostrou que o log de um número não nulo tem infinitos valores, os quais são todos imaginários no caso do número ser negativo.

Boa parte dessas discussões envolviam argumentos metafísicos e não podemos dizer que Euler tenha esclarecido definitivamente a questão. Isso só ocorreu em 1 830 com Martin Ohm, o qual deu uma teoria completa para o calculo de a b e de ln a ( com a,b complexos ). Suas idéias foram divulgadas e estendidas por Cauchy , o qual elucidou a questão da multivocidade através das noções de ramo principal e ramos secundários de uma função.

Exemplo:

como e2 i = 1 , então ln ( e2  i ) = ln ( 1 ) mas é errado disso concluir que 2  i = 0.

Foi só com as idéias de Ohm e Cauchy que aprendemos a fazer o cálculo corretamente.

A aceitação dos números complexos:

Talvez possamos dizer que os principais matemáticos responsáveis por essa aceitação foram:

Lambert e Euler que estudaram o fechamento dos números complexos sob operações algébricas e transcendentes

Wessel que introduziu ( 1 797 ) a moderna representação geométrica, que foi depois popularizada por Mourey e Gauss c. 1 830.

Gauss que divulgou e muito usou essa representação e provou que os nmeros complexos sao necessários e suficientes para a Algebra ( Teorema Fundamental da Algebra: todo polinômio de coeficientes reais ou complexos pode ser fatorado em termos lineares, possivelmente complexos ).

Ohm e Cauchy que esclareceram a multivocidade das operações algébricas e transcendentes sobre os complexos.

Com isso, a terminologia desconfiada inicial ( n. sofísticos c. 1570, n. imaginários c. 1650 ) acabou cedendo lugar à mais natural denominação atual: números complexos, em c. 1830.  

Já no séc. dos 1800's os n. complexos encontraram grande uso no estudo da Mecânica de Fluídos, da Eletricidade e outros fenômenos em meios contínuos. Hoje, são instrumental absolutamente necessário em inúmeros campos da Ciência e Tecnologia.